Page 113 - progetto alice
P. 113
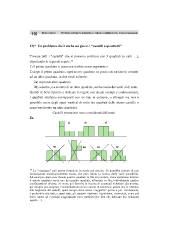
116 Mario Barra Problem solving di aritmetica e calcolo combinatorio. Concretizzazioni 23)* Un problema che è anche un gioco: i “castelli a quadretti” Trovare tutti i "castelli" che si possono costruire con 5 quadrati (o cubi …), 17 rispettando le seguenti regole: 1) il primo quadrato si pone con un lato su un segmento s 2) dopo il primo quadrato, ogni nuovo quadrato va posto con un lato in comune ad un altro quadrato, in due modi soltanto: 2a) sopra un altro quadrato 2b) a destra, o a sinistra di un altro quadrato, senza creare dei vuoti al di sotto. Quindi (è bene ripetere e indicare le regole con alcuni esempi e controesempi), i quadrati risultano sovrapposti con un lato in comune, o allineati ma non è possibile avere degli spazi vuoti al di sotto dei quadrati dello stesso castello o spazi vuoti sotto un altro quadrato). Castelli simmetrici sono considerati differenti. Es. sì sì sì no no no no 17 La “consegna” può essere formulata in modo più preciso. Si potrebbe trattare di una formulazione matematicamente esatta, che però limita la ricerca delle varie possibilità. Ad esempio, dopo aver fissato quattro quadrati in fila orizzontale, viene spontaneo mettere il quinto quadrato sopra uno dei quattro quadrati, affiancati in fila, individuando quattro configurazioni diverse. Si vuole poi favorire la ricerca di eventuali soluzioni già trovate, per rendere più semplice l’individuazione di un criterio di selezione: quello che si riferisce alla larghezza dei castelli, quasi sempre deve essere “suggerito” prima o poi. Ovviamente, è preferibile che tutti, o quasi tutti, gli studenti risolvano il problema, ricorrendo, come già detto, anche ad eventuali suggerimenti poco espliciti (due dita che indicano due soluzioni uguali, …).